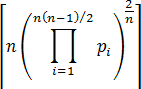A 60-Second Review of Graph Theory Terminology
A "graph" is a collection of "nodes", some pairs of which are connected
by an "edge".
If every pair of nodes is connected by an edge, the graph is called a
"complete graph". The complete graph with
n
nodes is denoted by
Kn.
We can associate a value, called a "weight", with each edge.
Some examples:
 A graph
A graph
 A graph with weighted edges
A graph with weighted edges
 K4
K4
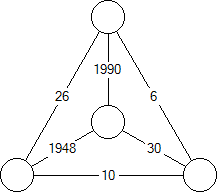 K4 with weighted edges
K4 with weighted edges
The Contest
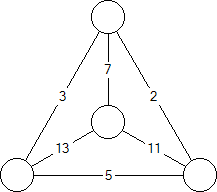
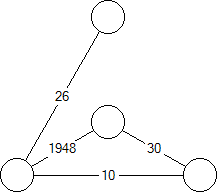
For a graph where every edge has a weight, we define a node's "energy" to
be the product of the weights of the edges attached to it. We also
define the energy of the graph to be the sum of the node energies.
For example:
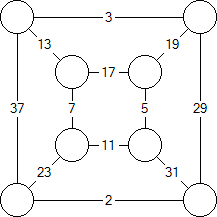 1. Start with edge weights
1. Start with edge weights
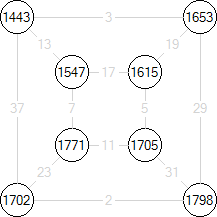 2. Then calculate node energies
2. Then calculate node energies
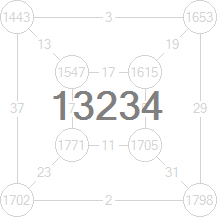 3. Then calculate graph energy
3. Then calculate graph energy
In this contest you are asked, for each value of
n
from 4 to 28 inclusive, to weight the edges of
Kn
using the first
n(n-1)/2
primes. Your goal is to create and submit graphs with the smallest possible energy.
For each value of
n
you can submit more than one graph,
but only your best graph will count.
See How to Enter,
below, for instructions on how to submit graphs.
See The Scoring System, below, to
learn how we determine the winner.
This contest was inspired by Stan Wagon's Problem of the Week 1241
Petersen Graph with Small Labels.
The Prizes
First prize: Any item, up to a $500 value, from Bathsheba Sculpture.
Second prize: Any item, up to a $100 value, from the same site.
How to Enter
Just paste your graphs into the large box on the
Submit page and click the Submit
Entry button. Format your graphs as follows:
-
Represent a graph by a comma-delimited list of nodes.
-
Represent a node by a comma-delimited list of edge weights enclosed in curly braces.
-
To submit more than one graph at a time,
separate them with semicolons.
Do not put a semicolon after your last graph.
-
Include spaces and line breaks anywhere you like (except within a
number) to improve readability.
For example, if you wanted to submit this graph:
you could enter:
{2, 3, 7}, {2, 5, 11}, {3, 5, 13}, {7, 11, 13}
Look! A box! There must be something really important here!
This web site uses a server with very limited resources, so please
make a reasonable effort to submit only graphs that improve
on the graphs you've already submitted. If you are wondering
what constitutes "reasonable", consider the following:
-
It is reasonable that while you are debugging you will submit
some graphs that aren't improvements.
-
It is reasonable that you will occasionally submit a
non-improvement by accident.
-
It is not reasonable that you routinely submit
graphs without knowing if they are improvements.
-
It is not reasonable that, whenever
you find an improved graph for some
n,
you submit all 25 of your best graphs
even though only one is an improvement.
Your cooperation is greatly appreciated.
The Scoring System
The Formula
The entrant with the highest contest score wins.
Here's how we calculate your contest score:
-
For each of the 25 values of
n,
there is a target energy.
The formula for calculating target energies is in the
FAQ
section, below.
-
For each of the 25 values of
n,
we find your best graph. Your raw score for that
n
is the amount by which the graph's energy exceeds the target energy.
-
For each of the 25 values of
n,
we compute a subscore from 0 to 1.
We do this by dividing your raw score for that
n
into the smallest raw score for that
n
by any entrant.
-
Your contest score is the sum of your 25 subscores.
If two entrants have the same contest score, we break
the tie by giving preference to the entrant whose last
improvement was submitted least recently.
An Example
Let's walk through a simplified example. Suppose that we modify
the contest by asking you to submit graphs for only three values of
n: 4, 5 and 6.
The target energies are:
|
4 nodes |
5 nodes |
6 nodes |
| Target energy |
694 |
42008 |
5102117 |
Further suppose that we have 3 entrants (Elizabeth,
Angelica and Peggy) and that their best graphs have these energies.
|
4 nodes |
5 nodes |
6 nodes |
| Elizabeth |
800 |
60000 |
8000000 |
| Angelica |
1000 |
50000 |
7000000 |
| Peggy |
900 |
70000 |
6000000 |
The entrants' raw scores are therefore:
|
4 nodes |
5 nodes |
6 nodes |
| Elizabeth |
106 |
17992 |
2897883 |
| Angelica |
306 |
7992 |
1897883 |
| Peggy |
206 |
27992 |
897883 |
We note the smallest raw score for each value of
n,
as follows:
|
4 nodes |
5 nodes |
6 nodes |
| Smallest Raw Score |
106 |
7992 |
897883 |
Finally, we compute the subscores and contest score for each entrant:
|
4 nodes |
5 nodes |
6 nodes |
Contest Score |
| Elizabeth |
106 / 106 = 1.000 |
7992 / 17992 = 0.444 |
897883 / 2897883 = 0.310 |
1.754 |
| Angelica |
106 / 306 = 0.346 |
7992 / 7992 = 1.000 |
897883 / 1897883 = 0.473 |
1.820 |
| Peggy |
106 / 206 = 0.515 |
7992 / 27992 = 0.286 |
897883 / 897883 = 1.000 |
1.800 |
Angelica has the highest contest score and therefore wins.
A shout-out goes to the first person who,
without resorting to
Google, Wikipedia or any other information source (online, physical,
human or supernatural),
can tell us who Elizabeth, Angelica and Peggy are.
Creative guesswork is encouraged. Post your answer in the
discussion group..
Getting Your Questions Answered
First, check the FAQ section below. If you can't
find the information you need there, send your question to the
discussion group.
If your question is of a personal nature, and not
of general interest, send an email directly to
Al Zimmermann.
The Discussion Group
If you think you might enter the contest, you should join the
contest discussion group. You can join either by sending a blank email
here or by visiting the group on
groups.io.
The discussion group serves two purposes. First,
it allows contestants to ask for clarifications to the rules. Be aware that
sometimes these requests result in changes to the rules, and the first place
those changes are announced is in the discussion group. Second, the discussion
group allows contestants to interact with each other regarding programming
techniques, results and anything else relevant to the contest.
My Lawyer Would Want Me To Say This
I reserve the right to discontinue the contest at any time. I reserve the right
to disqualify any entry or entrant for any reason that suits me. I reserve the
right to interpret the rules as I see fit. I reserve the right to change the
contest rules in mid-contest. In all matters contest-related, my word is final.
Frequently Asked Questions
-
Does every edge weight in a submitted graph have to be unique or can an edge weight be used multiple times?
In this contest every edge weight in a graph must be unique within that graph.
-
How are the target energies calculated?
The target energy for
n
is
where
pi
is the
ith
prime.
For example, the target energies for
n
= 1, 2, 3 and 4 are 1, 4, 29 and 694, respectively.
-
Can teams enter the contest?
Yes. But a team can only be formed by those who have not
already entered the contest as individuals. Once you enter
as an individual, team membership is no longer open to you.
Likewise, once you've joined a team you can't break away and
start submitting graphs on your own behalf.
If you would like to form a team, please follow these instructions:
-
If they do not already exist, create individual accounts for each team member.
Do not create a second account for any team member who already has one.
-
Let me know
each team member's registered email address. It is important that
no team member submit any entries to this contest until I notify you
that the team has been created and that it is okay to begin submitting.
-
After I've created the team, team members can submit entries to
the contest from their individual accounts. The contest engine
automatically intercepts these entries and diverts them to the
team account. The team is listed on the standings page.
-
Note: Teams are contest-specific. Joining a team for this
contest does not affect your participation in other contests.
-
May I write a program that submits entries by bypassing my browser?
Yes and no. If your program keeps track of your submissions and only submits
improved graphs, yes. Otherwise, no. For the Son of Darts contest a
few years ago, there was one participant who wrote a program to exhaustively
generate all possible solutions and submit every one of them. Within two weeks
he'd submitted over a million entries. The AZsPCs database had grown to 10
times its normal size and this individual was single-handedly responsible for
90% of the entries in the database. Please compute responsibly.
-
I've written a little program that draws graphs and
highlights the nodes with the highest and lowest energies.
May I distribute the executable to other contestants?
No. This is a programming contest and writing useful tools
is something a programmer should be able to do for himself.
That alone is sufficient reason to disallow the distribution
of such tools, but consider also that you'd be disadvantaging
those who don't hear about your tool and those who can't run
your executable in their environment.
-
What topics are appropriate for the discussion group?
With only one exception, if it's related to AZsPCs then
it's fine to talk about it in the discussion group. The
exception is spoilers. Spoilers include:
- specific graphs
- detailed algorithms
If you are not sure if something would be considered a spoiler,
ask me.
-
After I submit a graph, the scorer shows me the
graph's "canonical representation". What is that?
To create a canonical representation of a graph,
the scorer sorts its nodes by their energy and the node's
edges by their weight. Representing graphs canonically
makes it easier to notice when two seemingly different
graphs are fundamentally the same.
-
Why is this contest called Primorial Soup? Did you mean Primordial with a 'd'?
Primorial is a mathematical function. The primorial of
n
is the product of the primes less than or equal to
n.
It is written
n#.
Check it out at
Mathworld.
|